2023. 9. 21. 14:16ㆍBlockchain/Roll up
Roll up Series
[Blockchain/Roll up] - Rollup의 개념과 특성
[Blockchain/Roll up] - ZK rollup - 1. 목적/library
[Blockchain/Roll up] - ZK rollup - 2. ZKP
[Blockchain/Roll up] - ZK rollup - 3. zkEVM 프로젝트
[Blockchain/Roll up] - ZK rollup - 4. zk-SNARK의 Circuit & QAP
앞선글에서 zk rollup으로 L2를 구현 시 EVM 호환성이 힘들다는 언급을 한적이 있다. EVM의 로직 처리에 대해 모두 구현하는 것이 힘들다는 것이 이유인데, 이번 글에서는 zk-SNARK 적용 시에 어떠한 과정이 숨어 있기 때문에 힘든 것인가를 확인하는 포스팅을 진행하려 한다. 이 글은 Vitalik의 QAP에 대한 글을 참고로 작성되었다. 큰 흐름을 보기위해 자체적으로 생략한 부분도 있고, 중간중간 확인이 필요한 부분과 계산 상 넘어간 부분을 조금 더 보강하여 작성하려 한다.
zk-SNARK Pipeline

zk-SNARK는 아래와 같은 파이프라인을 거쳐 특정 문제(problem)에 대한 연산 과정(computation)이 zk-SNARK를 통해 zk proof가 생성된다. 직접적인 연산 과정을 zk-SNARK에 적용할 수 없기 때문에 연산을 할 수 있도록 문제를 변환시켜야 하는데, 이 변환시킨 형식이 QAP(Quadratic Arithmetic Programs)이다.
파이프라인을 말로 풀어본다면,
- 문제를 표현하기 위해 회로(circuit) 구축: 문제의 논리화
- 회로에서 R1CS를 생성: 수학적 형식으로 변환
- R1CS를 QAP로 변환: 다항식으로 변환
- QAP의 linear PCP/linear interactive proof 변환: 검증 가능한 형태로 변환
- Proof에서 zk-SNARK: SNARK로 컴파일
으로 확인할 수 있다. 이 포스팅에서는 비탈릭 부테린의 자료를 참고로 QAP까지의 과정만 확인할 것이므로 문제부터 QAP까지에 대한 전반적인 내용을 확인하려 한다.
Problem
앞선 ZKP에 대한 설명으로부터 문제에 대해 정의해본다. 해당 글의 장 자크 키스케다의 예제를 참고하자.
증명자(prover)가 검증자(verifier)에게 직접 key의 실물을 보여주지 않고도 동굴 내부의 문을 열 수 있다는 것을 증명하는 것이 ZKP라고 하였다. 이 때의 "문"이 바로 연산을 위한 문제이다. 정확히 말하자면, 검증자가 요청한 결과 대로 증명자가 A 또는 B로 나오는 과정을 문제라고 할 수 있다.
zk-SNARK에 적용하기 위한 이 문제는 아무것이나 선택해서는 안되며 비결정론적 튜링 기계(NTM; Nondeterministic Turing Machine)로 다항 시간(polynomial time algorithm) 내에 풀 수 있는 문제들로만 선택되어야 한다.
즉 이 문제는 NP(Nondeterministic Polynomial time) class에 포함되어야 한다.
NP class
NP를 위키에 검색 해보면 "비결정론적 튜링 기계로 다항 시간안에 풀 수 있는 판정 문제의 집합"으로 나와있다.
여기서 "비결정론적 튜링 기계"란 어떤 문제에 대해 같은 입력으로도 여러 출력을 낼 수 있는 기계를 말한다. 즉, 특정 상태에서 변화될 수 있는 상태가 하나로 정해져 있지 않은 경우를 말한다.
"다항 시간"이란 어떤 문제를 계산하는데 걸리는 시간이 문제의 크기 n이 주어질 때 n의 다항식 함수보다 크지 않는 것을 말한다. 즉, 시간 m(n)에 대해 m(n)=O(nk)로 표현할 수 있으며, 지수 시간 2O(n) 등 초다항 시간보다 (비교적) 짧은, "빠른 시간"을 말한다.
이것을 필자 나름대로 간략하게 풀어서,
"특정 입력을 통해 빠른 시간 내에 특정 결과가 나온다는 것을 증명할 수 있다면 어떤 문제는 NP class에 속한다."
라고 정의 하려 한다.
예를 들어 보자. 집합 {1, 2, 3, 4, 5 ... n}으로 주어진 집합이 있을 때 이 집합의 부분집합 중 원소의 합이 10인 집합이 존재하는가? 라는 물음에 있어서 확실하게 답을 할 수 있는 다항 시간 알고리즘을 알 수 없다.
하지만 {2, 3, 5}라는 부분집합을 알려주고 다시 물음을 한다면, 해당 부분집합이 본래 집합의 부분 집합이라는 것을 쉽게 확인할 수 있고, 각 원소를 더해 10임을 확인할 수 있으며, 이는 다항 시간 내에서 오랜 시간이 걸리지 않기 때문에 이 문제는 NP class라고 할 수 있다. {2, 3, 5}가 "특정 입력"이며, 존재한다는 결과가 "특정 결과"이며, 다항 시간이 "빠른 시간"으로 대응될 수 있다.
왜 zk-SNARK를 적용하는데 NP class에 속하는 문제를 골라야 하냐는 물음은 NP를 간략하게 풀이한 위 문장으로 해석될 수 있을듯 하다.
특정 입력은 동굴 예제에서의 key가 되고, 특정 결과는 검증자가 요청한 문으로 나오는 행위를 뜻할 때, 이 결과가 나오는 것이 확실해야지만 검증 과정이 의미가 있을 것이고,
특정 결과가 나올 것이라는 것이 확실해야 검증자가 특정 입력을 직접 보지 않더라도 특졍 결과만 확인하여 특정 입력을 증명자가 가지고 있다는 것을 검증할 수 있을 것이다.
또한 빠른 시간의 검증 시간이 있어야만 검증을 효율적으로 할 수 있을 것이다. 초다항 시간 내의 검증은 의미가 없을 것이다.
Algebraic Circuit
앞으로의 설명은 Problem(문제)를 한 예제와 함께할 것이며, 간단한 3차 방정식 x3+x+5를 그 문제로 삼는다. 이에 대한 function은 아래와 같다.
def qeval(x):
y = x**3
return x+y+5이 로직을 수학적 회로(circuit)로 Flattening하여 일련의 제약 조건으로 작성을 해야 한다. 다항식이 복잡할수록 이 flattening 절차가 굉장히 어려워 진다. 위 코드의 flattening process 결과는 아래와 같을 것이다.
sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5각 식은 2개의 input wire, 1개의 output wire로 구성이 되어야 한다. 위 4가지 식은 각각 회로의 로직 gate로써 처음부터 순차적으로 gate를 통과한다면 최종 결과 ~out이 출력될 것이다.
R1CS

구성한 회로를 R1CS(Rank-1 Constraint System)로 변환한다. 3개의 벡터(a,b,c)로 구성된 그룹의 시퀀스이며, R1CS의 해(solution)는 벡터 s 를 만족시켜야 한다. 여기서 벡터 s와 내적(dot product)한 초기 벡터 (a,b)의 곱은 s와 c의 내적과 같아야 한다.(s⋅a×s⋅b=s⋅c)
∴
추가로, 그림에서 표현된 [1, 3, 35, 9, 27, 30] 가 벡터 s를 뜻한다.
Create verctor
위에서 선언했던 로직 게이트를 구현하기 위한 벡터를 구성할 차례이다. 먼저 벡터의 변수들은 아래와 같이 매핑된다.
'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'x나 ~out등은 flattening된 식에서 확인을 할 수 있고, ~one의 경우 숫자 1을 나타내는 더미(dummy) 변수이다.
솔루션 벡터는 이 변수들을 적절히 할당해야 하는데, 논리 게이트 식에서 영향을 받는 변수들만 할당해야 한다.
첫번째 게이트인 sym_1 = x * x의 솔루션 벡터는 아래와 같이 설정 할 수 있다.
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]벡터 a에서 두번째 변수 x와 벡터 b에서의 두번째 변수 x가 1을 곱함으로써 활성화 되었고, 벡터 c의 네번째 변수 sym_1이 활성화 되었다. 각 벡터 변수들에 내적되는 s_i의 값과 상관없이 x * x - sym_1 = 0 로직이 위와 같은 솔루션 벡터로 표현된다.
두번째 게이트인 y = sym_1 * x는 아래와 같이 표현된다.
a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]두번째 게이트도 첫번째와 마찬가지로 게이트 식에 영향을 받는 변수들만 1을 곱함으로써 활성화 된 것을 알 수 있다.
세번째 게이트인 sym_2 = y + x는 아래와 같이 표현된다.
a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]동일 벡터 내의 변수들은 모두 합을 한다. 따라서 벡터 a의 두번째 변수 x와 다섯번째 변수 y가 1을 곱한 상태에서 활성화 되었고 같은 벡터 내에 있으니 이는 x + y를 뜻한다. 벡터 b는 숫자 1을 뜻하는 ~one이 활성화 되어 결국 (x + y) * 1 = sym_2가 된다.
네번째 게이트인 ~out = sym_2 + 5는 아래와 같이 표현된다.
a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]벡터 a에서 숫자 5를 표현하기 위해 ~one에 5를 곱해진 뒤 활성화 되었고, 여섯번째 변수 sym_2와 더해진다. 세번째 게이트 식과 비슷하게 위 솔루션 벡터는 결국 ~out = sym_2 + 5를 나타낼 수 있다.
이로써 R1CS 벡터들의 그룹 시퀀스 (A, B, C)는 아래와 같다.
A
a_1 = [0, 1, 0, 0, 0, 0]
a_2 = [0, 0, 0, 1, 0, 0]
a_3 = [0, 1, 0, 0, 1, 0]
a_4 = [5, 0, 0, 0, 0, 1]
B
b_1 = [0, 1, 0, 0, 0, 0]
b_2 = [0, 1, 0, 0, 0, 0]
b_3 = [1, 0, 0, 0, 0, 0]
b_4 = [1, 0, 0, 0, 0, 0]
C
c_1 = [0, 0, 0, 1, 0, 0]
c_2 = [0, 0, 0, 0, 1, 0]
c_3 = [0, 0, 0, 0, 0, 1]
c_4 = [0, 0, 1, 0, 0, 0]QAP
생성한 R1CS를 QAP로 변환해야 한다. 이제 생성한 벡터들을 다항식으로 구성된 그룹으로 변환하는 과정이 필요하다. 각 벡터의 순서는 x좌표로 표현될 수 있고, 벡터의 변수 값을 x좌표에 대응되는 y좌표라고 지정한다면, 각 벡터 변수는 특정 다항식의 (x,y)좌표라고 생각할 수 있을 것이다.
예를 들어 보자. 벡터 a_1은 x=1, a_2는 x=2... 이며, 첫번째 다항식의 y값들은 0, 0, 0, 5가 된다. (A의 새로로 보자.)
두번째 다항식의 x좌표는 첫번째와 동일하지만, y값들은 1, 0, 1, 0이 된다. 이 좌표들을 이용하여 라그랑주 보간법(Lagrange interpolation)으로 특정 다항식을 구할 수 있다.
Lagrange interpolation
라그랑주 보간법이란, (x_1, y_1), \cdots, (x_{n+1}, y_{n+1})의 좌표가 주어져 있을 때 이 점들을 모두 지나는 n차 이하의 다항식을 구할 수 있는 공식이다. 두 점 (x_0,y_0), (x_1,y_1)가 주어졌을 때 라그랑주 보간식은 아래와 같다.
y=\left( \frac{x-x_1}{x_0-x_1} \right)y_0 + \left( \frac{x-x_0}{x_1-x_0} \right)y_1
원리는 간단한데, x_0를 x에 대입하면 y_0에 곱한 항은 1이 되고 y_1에 곱한 항은 0이 되므로 (x_0,y_0)을 지날 수 있다. x_1을 대입한 경우는 출력되는 y가 반대가 될것이다.
실제 좌표를 이용하여 예시를 통해 확인해본다.
(1,3), (2,2), (3,4)가 주어져 있고, 이들을 통과하는 2차 다항식을 확인하려 한다. 먼저 (1,3), (2,0), (3,0)을 통과하는 다항식부터 만들어 본다. 단순하게, x=2, x=3에서 x절편을 갖는 식은 아래와 같다.
y=(x-2)(x-3)
이 때의 그래프는 아래와 같다.
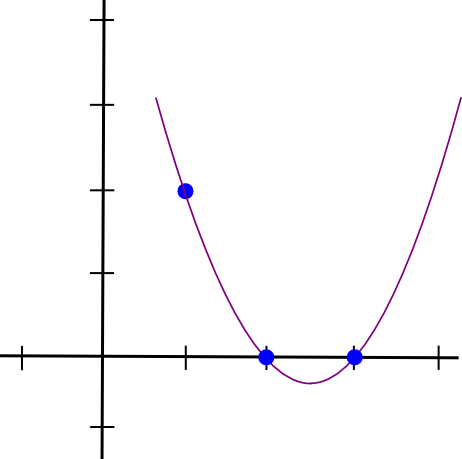
여기서 x=1일 때의 y좌표를 올바르게 지나가도록 하는 식은 아래와 같다.
y=\frac{(x-2)(x-3) \times 3}{(1-2)(1-3)}
이를 통해 y=1.5x^2-7.5x+9의 식을 얻을 수 있다. 이 때의 그래프는 아래와 같다.
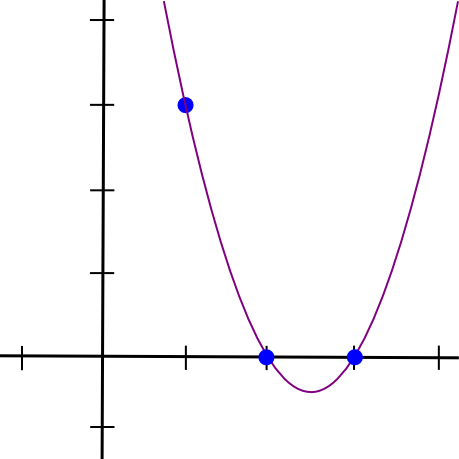
나머지 두 점에서도 동일한 작업을 수행하여, 최종적으로 y=1.5x^2-5.5x+7의 식을 얻을 수 있으며, 이 때의 그래프는 아래와 같다.
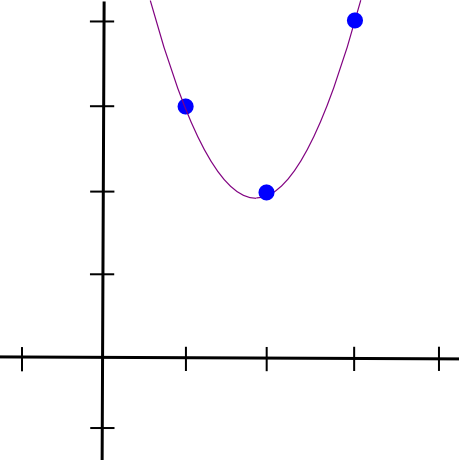
R1CS to QAP
라그랑주 보간법을 통하여 원하는 3차 다항식으로 만들어야 한다. 벡터 그룹 A의 가장 첫번째 다항식부터 확인해 보도록 하자.
우리는 이전에 벡터의 순서와 대응되는 값으로 좌표를 만들 수 있다고 확인했다. 이 때 A의 각 벡터 첫번째 좌표들을 확인하면 아래와 같을 것이다.
A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]
(1,0)
(2,0)
(3,0)
(4,5)이 때의 보간법은 한 점을 제외한 나머지 점들의 y가 0이므로 굉장히 쉽게 다항식을 만들 수 있을 것이다.
\frac{(x-1)(x-2)(x-3)}{(4-1)(4-2)(4-3)} \times 5 로 표현될 수 있을 것이며, 결국 아래와 같은 식이 된다.
\frac{5}{6} (x-1)(x-2)(x-3)
= \frac{5}{6} (x^2-3x+2)(x-3)
= \frac{5}{6} (x^3-6x^2+11x-6)
= 0.833x^3-5x^2+9.166x-5
이를 오름차순으로 각 계수에 대한 행렬로 나타내면 아래와 같이 표현될 수 있을 것이다.
[-5.0, 9.166, -5.0, 0.833] 모든 벡터에 대해 보간법을 적용하여 다항식을 계산한 결과는 이미 Vitalik이 계산해 놨으니 그대로 가져온다.
A polynomials
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]
B polynomials
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
C polynomials
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]테스트를 위해 x=1에서 확인해 본다. 다항식에서 x=1은 결국 모든 계수를 더하는 것이므로, 어렵지 않게 계산될 수 있다.
A results at x=1
0
1
0
0
0
0
B results at x=1
0
1
0
0
0
0
C results at x=1
0
0
0
1
0
0결과는 첫번째 게이트를 만들었을 시의 벡터 (a, b, c)에 대한 결과와 같은것을 확인할 수 있다.
a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]Checking the QAP
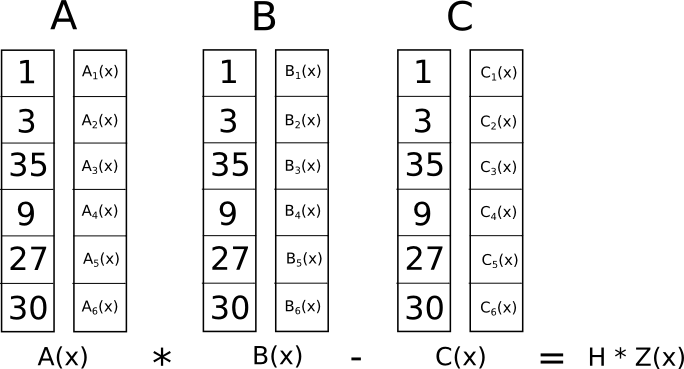
위에서 게이트를 나타내기 위해 사용한 모든 x좌표를 대입하여 확인한 결과가 0이라면 모든 체크가 통과됨을 의미한다. x좌표 중 하나라도 검사 결과가 0이 아닌 값이 나오는 경우는 입력 값이 틀렸다는 의미가 된다.
QAP로 도출된 다항식에 하나하나 x좌표들을 대입하여 검증할 수 있으나, R1CS의 제약 조건인 4개의 게이트 식들을 개별적으로 확인하는 대신에 다항식에 대한 내적 검사(dot product check)로 모든 제약 조건을 동시에 확인할 수 있다.
위 그림에서처럼 내적 검사는 다항식의 사칙연산으로 이루어져 있기 때문에 결과도 다항식이 될 수 있다. 결과 다항식은 t = H(x)Z(x)로 일단 표현하자. 그러면 전체 식은 아래와 같다.
t=H(x)Z(x)=(s \cdot A)(s \cdot B)-(s \cdot C)
Z(x)는 논리 게이트들에서 0이 될 수 있는 다항식이며 아래와 같이 정의 될 수 있다.
Z(x)=(x-1)(x-2)(x-3) \cdots
H(x)가 어떠한 값을 가지고 있더라도 게이트에서 0이 되는(=Z(x)가 0이 되는) x가 대입 되었을 때 t=0이 되며, H(x)Z(x)+R(x)처럼 추가로 더해지는 R(x)가 없다면 모든 게이트에서 t는 0이 될 것이다.
즉 t=A \cdot s \times B \cdot s - C \cdot s가 정확한지 확인하기 위해 모든 게이트 단에서 확인할 필요는 없고, t를 Z(x)로 나누었을 때 나머지가 없다면 정상적이라 판단할 수 있다.
그림에서 처럼 선언된 벡터 s들을 벡터 그룹들과 연산해보자. 먼저 s의 첫번째 값 s_1은 A_1(x)와 곱해질 것이고 s_2는 A_2(x)와 곱해질 것이다. 그렇게 계산하면 각 벡터 그룹은 아래와 같은 식으로 표현 될 수 있다.
s \cdot A = \left( \sum_{i=1}^n s_i \cdot A_i(x) \right)
s \cdot B = \left( \sum_{i=1}^n s_i \cdot B_i(x) \right)
s \cdot C = \left( \sum_{i=1}^n s_i \cdot C_i(x) \right)
위 식을 통하여, 이전에 계산된 A, B, C 다항식과 벡터 s의 연산 결과에 대한 계수는 아래와 같다.
A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]t 다항식은 아래와 같이 나타낼 수 있다.
t=\left( \sum_{i=1}^n s_i \cdot A_i(x) \right)\left( \sum_{i=1}^n s_i \cdot B_i(x) \right)-\left( \sum_{i=1}^n s_i \cdot C_i(x) \right)
위 식으로 t를 연산시 확인 되는 계수는 아래와 같다.
t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]각 게이트에서 0이 되는 Z(x)는 Z(x)=(x-1)(x-2)(x-3)(x-4) 이므로, 계수는 아래와 같다.
Z = [24, -50, 35, -10, 1]다항식 나눈 결과는 아래와 같다.
h = t / Z = [-3.666, 17.055, -3.444]결과적으로, t를 Z(x)로 나누었을 때 나머지가 생기지 않았으므로 올바른 QAP solution임을 확인할 수 있다. 만약 R1CS의 솔루션 변수인 벡터 s의 한 값을 위조한다면 (e.g. s의 마지막 값을 30에서 31로 변경) 검사를 실패할것이다. x=3에서 결과는 0이 아닌 -1이며, t를 Z(x)로 나누었을 때 나머지가 생긴다(나머지 = t/Z=[-5.0, 8.833, -4.5, 0.666]).
Conclusion
zk rollup을 위한 zk-SNARK를 적용시 EVM 호환성이 떨어지는 문제가 발생하는 것에 대한 이유를 살펴보기 위해 zk-SNARK를 구현하는 과정 중 일부에 대하여 살펴보았다. 간단한 다항식을 이용하여 논리 게이트를 설계하고 이를 수학적 연산이 가능한 모델로 변환하는데에도 복잡한 과정을 거치는데, 더욱 복잡한 컨트랙트 로직, 상호 작용이나 체인 내 암호학적 작용을 증명하는 논리 게이트 및 회로를 설계하는것은 굉장히 힘든일이다.
zk-SNARK에 대한 동작 일부분을 확인했지만, Vitalik의 글을 가져오며 생략한 부분이 많다. 위 플로우에 대해 좀 더 상세한 설명을 원한다면 참고로 첨부한 해당 글을 확인하면 좋을것 같다.
참고
https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
https://en.wikipedia.org/wiki/NP_(complexity)
https://crypto.stackexchange.com/questions/87371/how-to-construct-a-circuit-in-zksnark
https://ko.wikipedia.org/wiki/%EB%9D%BC%EA%B7%B8%EB%9E%91%EC%A3%BC_%EB%8B%A4%ED%95%AD%EC%8B%9D
'Blockchain > Roll up' 카테고리의 다른 글
| ZK rollup - 3. zkEVM 프로젝트 (0) | 2023.09.21 |
|---|---|
| ZK rollup - 2. ZKP (0) | 2023.06.15 |
| ZK rollup - 1. 목적/library (0) | 2023.06.15 |
| Rollup의 개념과 특성 (0) | 2023.06.14 |